Introduction

Ethereum’s vision is to be a secure and scalable decentralized backbone of the modern economy. One major step toward achieving this vision is the integration of zkEVMs into the Ethereum protocol.

In this book, we explore this idea in depth - what zkEVMs are, how they can be applied to Ethereum, and how theoretical advances in cryptography, combined with significant engineering effort, make zkEVMs a reality.

Slots, Re-Execution and Gas

One of Ethereum’s core functionalities is maintaining consensus on a shared state in a decentralized way. To achieve this, Ethereum operates in discrete time intervals called slots, during which the blockchain’s state can be updated at most once. In each slot, participants in the Ethereum protocol work to agree on a state transition, which is represented by a block. Each block contains, among other things, a list of transactions. Here, a transaction isn’t just a monetary transfer - it can be any programmatic action, such as calling a smart contract function that executes code and potentially alters the shared blockchain state. Intuitively, the more transactions included in a single block, the lower the amortized overhead imposed by the consensus algorithm per transaction.

A simplified version of what happens in a slot is as follows:

A proposer is selected and distributes a signed block of transactions over the gossip network.
Other participants, called validators, independently re-execute the transactions in the block to verify its correctness. If the block is valid, they generate and distribute attestations.
Once enough attestations are collected, the block is considered confirmed or finalized by consensus (ignoring many details here).

To ensure that this verification process completes in a timely manner, Ethereum imposes limits on how much computation can occur per block. This is where the concept of gas becomes essential.

Gas is a unit that measures the amount of computational effort required to execute a transaction or smart contract on Ethereum. Each operation has an associated gas cost. When you submit a transaction, you specify a gas limit (the maximum you’re willing to spend) and a gas fee (what you’re willing to pay per unit of gas). If the transaction runs out of gas, it fails, but still consumes all the gas spent up to that point.

More importantly, there is also a block gas limit, which caps the total gas that can be consumed by all transactions in a block. This upper bound is essential to ensure that the validator’s re-execution can be completed in time. It also effectively limits Ethereum’s throughput: only a certain amount of computation can happen per block.

Scaling Naively

One might think that increasing the block gas limit would immediately solve Ethereum’s scalability issues: more gas per block means more transactions, which means higher throughput. However, recall that all validators must re-execute the block to verify its correctness within the fixed duration of a slot. Raising the gas limit naively increases the computational load on validators. One way to address this is by requiring validators to have more powerful hardware. However, this approach has limits: if hardware demands become too high, it raises the barrier to entry for validators, undermining decentralization.

Thus, a fundamental bottleneck in Ethereum’s scalability is that every validator must re-execute every transaction.

zkEVMs to the Rescue

Fortunately, zkEVMs offer a powerful solution to this bottleneck. They rely on a cryptographic tool known as a succinct non-interactive argument of knowledge (SNARK). The key idea is simple: instead of requiring all validators to re-execute every transaction, we allow a single party, typically the proposer or a specialized prover, to execute the block and generate a short cryptographic proof that shows the correctness of this execution. This proof is then included with the block. Importantly, verifying this proof is much cheaper than re-executing the entire block. By verifying the proof instead of re-executing every transaction, validators dramatically reduce their computational and hardware demands. This allows Ethereum to safely raise the gas limit — and thus increase throughput — without compromising decentralization or validator accessibility.

Structure of this Book

This book is structured into four parts, two of which form the conceptual core:

Part I explains how a zkEVM can be used Ethereum. It explains what kind of problems it solves and how. In particular, here we treat the zkEVM as a magical black box with a specific interface and desired efficiency and security properties.
Part II explains the cryptographic principles underlying the construction of most zkEVMs. While different constructions of zkEVMs differ in details, most of them follow a common framework, which we outline in this part. This is not meant to be a complete tutorial on the construction of succinct argument systems. Instead, we keep it short and refer to existing works discussing the topic.
Part III contains sections that are tailored to specific audiences, e.g., Ethereum client developers, or readers interested in benchmarking.
Part IV tracks the current status of the zkEVM effort and is meant to be updated regularly.

Part I: zkEVMs in Ethereum

This book takes a top-down approach to exploring zkEVMs. Accordingly, Part I introduces zkEVMs abstractly and explains how they can be applied within the Ethereum protocol.

We begin by defining the syntactical interface and key properties of zkEVMs. From there, we treat them as a black box and examine the types of problems zkEVMs can address and how they provide solutions. In many cases, alternative approaches exist, but zkEVMs represent one compelling path.

While this section is designed to be as self-contained as possible, we assume the reader has a basic understanding of the Ethereum protocol.

zkEVM Interface

Before exploring how zkEVMs can enhance the Ethereum protocol, we first clarify what they are. Specifically, we define the functionality they offer by outlining their syntax and interfaces, as well as their security and efficiency properties. With this definition in place, we can treat zkEVMs as a black box throughout the remainder of this part. We invite the reader to take a pause after this section and think about which problems in Ethereum could be solved using zkEVMs.

Remark: We sometimes use the terms zkVM and zkEVM interchangeably, although they historically have a slightly different meaning: while a zkVM can prove the execution of a general program, a zkEVM was meant to prove the execution of the Ethereum Virtual Machine (EVM). Our definition is actually closer to a zkVM, but the programs that we input will be the state transition functions of Ethereum clients.

Intuition

At a high level, zkEVMs provide a proof of correct execution.

Imagine two parties: a computationally powerful prover, Alice, and a less powerful verifier, Bob. Both agree on a function f — for example, one implemented in Rust. They also share an input x and an output y, and Alice claims that f(x) = y.

How can Bob be confident this claim is correct?

Naive solution. Bob could re-execute f on input x himself, but this might be prohibitively expensive.
Succinct argument solution. Instead, Alice can produce a succinct non-interactive argument (SNARG), which convinces Bob that f(x) = y. “Succinct” here means that the argument is small in size and inexpensive to verify - much cheaper than full re-execution.

SNARGs are fascinating cryptographic constructs, and remarkably, they can be built efficiently and unconditionally in the random oracle model. For now, we treat SNARGs as given.

Importantly, SNARGs are non-interactive: Alice just sends a single convincing argument (or proof) to Bob and they do not need to interact back and forth. Especially, the proof that a single powerful prover Alice computes, can be used to convince arbitrarily many verifiers Bob.

Syntactical Interface

We now define the core interface that a zkEVM exposes:

Prepare(f) -> vk. This function takes as input a description of the program f and outputs a verification key vk. This key does not need to be kept secret. The Prepare step serves as a preprocessing phase, after which only the key vk must be retained. This can be advantageous: for example, vk is typically much smaller than the full description of f.
Prove(f, x) -> (y, proof). This function is executed by the Prover. It runs the program f on input x to compute the output y, and simultaneously generates a short proof (more precisely, a succinct argument) attesting that f(x) = y.
Verify(vk, x, y, proof) -> 0/1. This function is executed by the Verifier. It checks the validity of the given proof with respect to the verification key vk. It outputs 0 (for reject) or 1 (for accept).

Remark: When talking about zkEVMs in Ethereum, it is important to agree on a syntax first. In fact, a recent project aims to unify the syntax of existing zkVM implementations. The interface is only minimally more complex than what we have defined.

Properties

Now that we have a syntax at hand, we turn to the functionality, security, and efficiency properties that zkEVMs must provide. Namely, these are completeness (always can generate proofs for true statements), soundness (cannot generate proofs for false statements), and succinctness (proof is small and verification is cheaper than re-execution).

Remark: Despite what the name might imply, zkEVMs generally do not provide zero-knowledge in the cryptographic sense, i.e., the property of revealing nothing beyond the validity of the statement. This confusion stems from a misuse of the term “ZK” within large parts of the blockchain community, where it is often used synonymously with succinctness. However, zero-knowledge and succinctness are orthogonal properties that a proof system may or may not possess. For example, many systems studied in the literature are zero-knowledge but not succinct. In reality, zkEVMs would be more accurately described as succinct EVMs or SNARG-EVMs. Nevertheless, we adopt the term “zkEVM” in this book to remain consistent with prevailing community terminology, despite its technical imprecision.

Completeness

The most basic property that zkEVMs should have is completeness. Intuitively, it states that honestly generated proofs always verify. In particular, this will be essential for ensuring liveness when we use zkEVMs in Ethereum. Precisely, completeness means that the following always outputs 1, for any function f and input x:

vk := Prepare(f)
(y, proof) := Prove(f, x)
Output Verify(vk, x, y, proof) == 1 && y == f(x)

Soundness

We now turn to the main security property of zkEVMs, namely, soundness. It states that proofs for wrong claims must be rejected with overwhelmingly high probability. Note the complementary nature of completeness and soundness: the former defines a case in which a claim should be accepted, while the latter defines a case in which a claim should be rejected.

Let us make this more precise now. As common in cryptography, we define soundness via a probabilistic experiment (also called a game) that involves a hypothetical adversary Adv. The experiment for soundness is as follows:

Adv receives the system parameters, e.g., descriptions of hash functions that are involved.
Adv can do some computation and then output a claim and a proof, given by f, x, y, proof.
Adv wins the game, if f(x) != y (the claim is false) but Verify(vk, x, y, proof) == 1.

That is, an adversary breaks soundness and wins the game, if it can come up with a false claim accompanied by a verifying proof, i.e., if it can fool the verifier. Now, we say that a zkEVM is sound, if every efficient adversary has a negligible probability of winning in this game.

Remark: We do not specify exactly what the terms “efficient” and “negligible” mean, and refer the curious reader to the cryptographic literature. However, we want to make explicit that computationally unbounded (i.e., inefficient) adversaries may break the security of the scheme. This is why we should actually talk about arguments and not about proofs, but we treat the terms interchangeably for this book.

Remark: Note the adaptive nature of the soundness experiment: the adversary can choose the claim f,x,y after seeing the system parameters. This is an important detail.

Remark: Note that we can alway easily design a system that is complete but not sound, or vice versa: If Verify always outputs 1, the system is complete but for sure not sound. On the other hand, if it always outputs 0, the system is clearly sound but not complete.

Remark: Lower gas costs may attract even more users and applications, potentially bringing demand back towards capacity limits. zkEVMs could address this by pairing higher throughput with ongoing protocol upgrades (such as parallel mini-block execution and sharding) ensuring that capacity scales with adoption.

Threat of Prover Killer Blocks

Blocks containing extremely heavy or pathological workloads, so-called prover killers, can overwhelm provers, risking a stall in block finalization (liveness failure).

What makes a block a “prover killer”? Blocks containing operations whose on-chain gas costs don’t account for their proving complexity, i.e. cheap opcodes or interactions that incur heavy work at proof time but remain underpriced in gas.

Even the heaviest blocks are reduced to succinct proofs, shielding validators from worst-case workloads. Moreover, assigning proving responsibility to the block builder could align incentives. If builders generate proofs themselves, they would avoid constructing blocks that are too costly to prove. This mechanism preserves liveness and prevents network stalls.

Even if builders are responsible for proofs of their blocks, benchmarking how expensive opcodes are to prove is important as it could enable prover gas costs: costs in terms of gas units that resemble the relative costs of proving an opcode compared to the other opcodes. Censorship-resistance tools, like FOCIL, could then force builders to include transactions summing up to at least a certain amount of prover gas, while not capping the amount of prover gas provers may include (keeping all other constraints, like state growth, constant).

Big Picture: A Unified Execution-Validation Architecture

By cleanly separating execution (proving) from validation (proof checking), zkEVMs transform Ethereum’s scalability model:

Competitive execution market: Encourages specialized prover implementations to optimize speed and cost.
Massive validator diversity: Empowers lightweight nodes to secure the chain, strengthening decentralization.
Safe, elastic throughput: Allows base-layer capacity to grow without undermining security or validator accessibility.

Architecture

Note. Section under construction

Stateless client
Stateful client
Two primary patterns have emerged for client integration (to be explored and discussed in more details)
- Separate clients: Stateless clients (CL+EL) connect to stateful peers over a network subprotocol. Execution and verification are decoupled but remain interactive.
- Embedded Clients: A single client combines consensus logic (CL) with a lightweight embedded EL verifier (e.g. a zkVM or stateless executor). It receives blocks and proofs via gossip and verifies locally.
we could use https://hackmd.io/@oK3in1lRQ7-pt7b3j8nQxg/Hk9KBHsGgg here.

Same Slot Proving

A block must be proven within the slot it is proposed. A proposed slot architecture is that the builder must prove its own block. In the following we explore what a slot may look like under both Delayed Execution (EIP-7886) and enshrined Proposer-Builder Separation (ePBS EIP-7732). One of these two designs will likely be chosen to be included in the Glamsterdam upgrade. The time stamps proposed here are only an indication and are likely to be changed in the future based on testing. For more information, see the Same Slot Proving proposal.

Note that in the designs below, we assume that proofs are stored off-chain, however, the design could easily be changed to include proofs onchain. The roles of the beacon proposer and the builder stay very similar with zkEVMs as they are today. The differences are that a beacon proposer may have to include a flag indicating availability of proofs. Builders are responsible for sourcing proofs from provers. The new important role is a prover: the party that proves a block with a particular proving system.

Same Slot Proving under Delayed Execution

Slot n, t=0: The builder of slot n propagates the block (including the beacon block and execution payload) and its blobs.
Slot n, t=1.5: Attesters statically validate the beacon block.
Slot n, t=10 (Proof Deadline): Attesters freeze their view of available proofs. Provers must have propagated their proofs before this deadline.
Slot n+1, t=0: The builder of slot n+1 indicates whether the proofs were valid and timely with a flag in the block.
Slot n+1, t=1.5: Attesters verify the proofs. If attesters saw a valid proof by the proof deadline, but the builder indicated otherwise, they do not vote for block.

Same Slot Proving under ePBS

With ePBS, the beacon block and execution payload are separate objects sent by the beacon proposer and the builder respectively. A proof is necessary for the execution payload. No proof is required for the beacon block. With ePBS, there is no timeliness flag necessary for the proofs of the previous block since a beacon proposer does not build on a late execution payload. Therefore, building on an execution payload is an implicit flag of proof timeliness.

Slot n, t=0: The beacon proposer of slot n propagates a beacon block that commits to an execution payload hash.
Slot n, t=1.5: Attesters vote for the beacon block.
Slot n, t=10: The Payload-Timeliness Committee (PTC) votes for the availability of the execution payload, the blobs, and the proof. Provers must have propagated their proofs before this deadline.
Slot n+1, t=0: The beacon proposer of slot n+1 builds on the beacon block and execution payload of slot n if both were available, and there is a valid proof for the execution payload.
Slot n+1, t=1.5: Attesters verify the proofs. If the PTC voted for the availability of all necessary objects, attesters only vote for the beacon block of slot n+1 if it builds on the beacon block and execution payload of slot n.

Incentives

Robust incentive structures are necessary to ensure zkEVMs can be implemented on Ethereum. In this section, we highlight the main incentive problems that need to be addressed. Some of these problems may also be considered protocol architecture questions whose method of analysis usually benefits from a resource pricing viewpoint which is why they are included in the Incentives chapter.

Fallback Provers

At all times, there has to be at least one prover willing and able to prove blocks. That is, proving requires a 1-out-of-N trust assumption. The goal of the “Fallback Provers” project is to ensure this 1-out-of-N trust assumption is credible. Credibility is obtained by:

Ensuring the required costs of proving are low enough such that many people could run a prover.
Ensuring provers can be spun up quickly, whether locally, in a distributed setting, or with rented GPUs.
Ensuring new provers can be found by block builders.

This project is concerned with the third point and aims to build a robust in-protocol system to facilitate new provers and builders to communicate with each other, sometimes called multiplexing. The Fallback Provers project is a bottleneck for zkEVM adoption and therefore high priority.

Prover Killers

Prover killers are blocks that are excessively hard to prove due to the large number and/or types of transactions in the block. If blocks cannot be proven, but proofs are required to validate blocks, Ethereum cannot process transactions: it loses liveness. This project is also a bottleneck for zkEVM adoption, however, the solution space is better understood than that of the fallback provers project.

This project is concerned with preventing liveness issues due to prover killers. The two ways currently explored to do so are:

Assigning responsibility of proving a block to the builder of the block. The builder is then not incentivized to create a prover killer. (See the “Prover Killers Killer” post for the proposal).
Assigning proving gas costs to transactions based on how expensive they are to prove.

Note that these two methods are not mutually exclusive.

Prover Markets

It may be desirable to incentivize builders to source proofs from an open market of provers. For example, it may decrease barriers to entry to become a prover if it were otherwise hard to find a competitively-priced prover. This project is concerned with the following subquestions:

How important is it for Ethereum that there is an active and open market of provers in the normal case (that is, not the fallback case)?
What would an active and open market of provers in the normal case look like in-protocol?

This project is not necessarily a bottleneck for zkEVM adoption. Ethereum could maintain its liveness with just fallback provers without having a competitive prover market, therefore, this project is lower priority.

Censorship Resistance

zkEVMs leverage the asymmetry in computational power between a sophisticated prover and an unsophisticated validator set. Increased computation needed to build and prove blocks means it may not be possible for every validator to build a block locally. Ethereum may decouple throughput from local block building, which means it has to source its censorship reistance in another way than local block building. While FOCIL is a popular proposal to provide censorship resistance for regular transactions, a censorship resistance tool is still necessary for blobs. Francesco has made initial explorations on blob censorship resistance via mempool tickets, see here and here, and a more concrete proposal from Mike and Julian here.

Offchain or Onchain Proofs

Proofs can live either on- or offchain. Offchain proofs may have benefits such as reduced storage costs and potentially more verifier flexibility. The benefits and drawbacks of on- or offchain proofs must be better understood. Vitalik introduced the concept in this post, and Justin further explored it here.

Network throughput

zkEVMs remove the need for validators to re-execute transactions to verify a block. Still, some parties may want to re-execute (parts of) blocks, for example, to obtain the current state. There should still be limits to the amount of compute, and disk access necessary to execute the block. Moreover, the state growth must be limited as well. What the limits should be is, however, still unclear. This project aims to understand the potential increases in network throughput attributable to zkEVMs.

Preconditions for Integrating zkEVMs

Note. Section under construction

are there some changes that we need to make to the Ethereum protocol before we can move to zkEVMs?
What are the constraints to make this work in practice, e.g., how fast must proving be?
- define real-time proving here?
collect a list of open questions that we need to answer before we can have zkEVMs on L1

Real-Time Proving

A fundamental requirement for integrating zkEVMs directly into Ethereum’s base layer is real-time proving: the ability to generate a succinct validity proof for a block within the same slot time in which it is proposed (today, about 12 seconds).

Concretely, this means that after a block is fully assembled — including all transactions and state updates — a prover must generate a proof and share it with validators before the slot ends. The entire process, from finalizing the block contents to outputting and distributing the proof, must be completed within this tight time frame.

In this model, the block proposer first selects transactions from the mempool and assembles the block as usual. Once the block content is fixed, a zkVM runs the block execution logic and produces a compact zk proof attesting that all computations are correct. Validators then verify this succinct proof instead of re-executing the full block themselves.

Since the proof is typically finalized near the end of the slot, validators can quickly verify it before moving on to the next block. This introduces a deferred execution check: validators no longer perform full execution upfront but rely on a proof that can be checked very quickly. Despite this shift, Ethereum’s liveness and finality guarantees are maintained because this check still occurs entirely within each slot.

The diagram below summarizes this real-time proving flow:

Real time proving

Why Real-Time Proving is Important

In Ethereum today, each validator fully re-executes all transactions in a block before attesting. zkEVMs aim to remove this redundancy by shifting execution to a single prover who produces a succinct proof, while validators verify it cheaply. However, for this paradigm to preserve Ethereum’s liveness and finality guarantees, proofs must be ready within each slot’s time budget.

If a proof arrives late — even by a few seconds — validators cannot attest immediately, leading to missed attestations, weaker finality, and increased vulnerability to reorgs. Worse, if slots are missed systematically, it undermines the security assumptions of the beacon chain and the overall Ethereum consensus.

Thus, real-time proving is an absolute requirement to replace re-execution at L1 and maintain the same block time and finality cadence.

A Standardized Definition for L1

To align the efforts of zkVM teams, a set of concrete targets that define real-time proving for L1 integration has been recently proposed. These standards ensure that provers are not only fast but also secure, accessible, and practical.

Latency: A proof must be generated in ≤ 10 seconds for 99% of mainnet blocks. This leaves a ~2-second buffer within the 12-second slot for network propagation.
Security: Proofs must provide at least 128 bits of security. An initial 100-bit level may be acceptable temporarily, but 128 bits is the long-term goal.
Proof Size: The final proof must be ≤ 300 KiB and must not rely on recursive wrappers that use trusted setups.
Code: The entire prover stack must be fully open source.

Technological Foundations

Achieving real-time proving relies on a combination of cryptographic and engineering advances. At the heart of this effort are special virtual machines called zkVMs, which allow us to run Ethereum’s state transition logic and produce a short proof that the computation was done correctly.

To make proofs fast enough, these zkVMs must be carefully designed to minimize unnecessary work and handle large blocks efficiently. In practice, proving a block requires breaking it into smaller parts that can be processed in parallel and then combined into one final proof. The final proof should also be small enough to be posted onchain.

Hardware plays a critical role as well. Today, proofs are typically generated using powerful multi-node setups equipped with many GPUs, but recent trends show rapid progress. Improvements in parallelization, recursion strategies, and specialized acceleration are pushing proof times lower each year.

Importantly, data preparation steps (like generating execution traces and Merkle paths) also require careful optimization to stay within the time budget. Advances in data fetching, caching strategies, and efficient state access mechanisms all contribute to enabling real-time performance.

Guarding Against Prover Killers

Real-time proving must also protect against so-called prover killer blocks, blocks that are very hard to prove (see Threat of Prover Killer Blocks). To prevent this, the protocol can set strict time limits for when proofs must be submitted. This forces block builders to make sure their blocks can be proven quickly, avoiding blocks that might slow down or stop the network.

Toward Future Slot Times

Ethereum’s long-term roadmap envisions reducing slot times (for example to 6 seconds or even lower), which means proofs will need to be generated even faster. zkEVMs must guarantee that proofs are always ready within these tighter time frames, even for the heaviest blocks — not just on average.

Recent advances show that proving technology is evolving very rapidly. As slot times shorten, proving systems are expected to keep improving in parallel, aiming for proofs in 6 seconds, 3 seconds, or even under 1 second in the future. This makes fast proving a moving target that will continue to push technical progress forward.

Decentralization and “Home Proving”

Beyond speed, real-time proving has critical consequences for decentralization. If proof systems require massive GPU clusters or expensive specialized hardware, only a few large operators could run them, introducing new centralization risks.

To address this, the concept of “home proving” has become a key goal. This is the effort to make provers so efficient that solo stakers can run them from home, preventing a reliance on a few large, centralized operators. To make this goal tangible, the standardized definition for L1 provers includes specific constraints on hardware and energy costs:

On-prem Capital Expenditure (CAPEX): ≤ $100,000 USD for the necessary hardware.
On-prem Power Consumption: ≤ 10 kW, a limit designed to fit within the power capacity of a standard residential home.

The ultimate goal is to make provers small and efficient enough to run on modest clusters, and eventually even on consumer-grade machines such as powerful desktops or laptops. By making home proving feasible, the network can maintain a high degree of censorship resistance and decentralization, allowing individuals, small organizations, or community groups to participate in proving and supporting a more open and resilient network.

Part II: zkVM Internals

Note. Section under construction.

in this second part of the book, we introduce the basic concepts that underlie the construction of zkVMs
that is, we answer the question “How do zkVMs work internally?”
of course, each zkVM team made different design decisions and the different zkVMs work in different ways
however, there are some shared core principles underlying their design, and we want to explain those briefly, and link to more detailed explanations of those
the goal is not that the reader learns exactly how a specific zkVM works, but rather that the reader gets a basic understanding (without much detail) of the basic concepts and can later dive deeper into details of a specific zkVM (which is not in the scope of this book)
we expand on this doc by Cody here (or in an overview subsection)

Instruction Set Architecture

A zkVM’s Instruction Set Architecture (ISA) defines the fundamental “language” understood by the virtual machine — that is, the set of basic operations (instructions) a program can use to manipulate data, control flow, and perform computation inside the zkVM.

In traditional processors, the ISA is designed to run as fast and efficiently as possible in silicon chips, minimizing energy and latency. By contrast, in a zkVM, the ISA must be optimized for succinctness and prover performance: the fewer and simpler the instructions, the fewer polynomial constraints and columns are needed to generate a SNARK proof, reducing prover cost.

At a high level, you can think of an ISA like a minimal “vocabulary” of actions a program can use. For example, in a simple ISA, a few core instructions might be:

ADD x, y: Add values in registers x and y.
JMP addr: Jump to instruction at address addr.
LOAD x, [addr]: Load a value from memory into register x.

A program is simply a sequence of these instructions. In a zkVM context, each instruction corresponds to certain algebraic constraints that must be satisfied in a proof, so the choice and design of instructions directly impact efficiency.

Choosing an ISA for a zkVM involves delicate trade-offs between prover efficiency, compatibility with existing compilers and developer tools, and ease of writing or understanding programs.

In this section, we explore the main approaches under consideration: general-purpose ISAs such as RISC-V and MIPS, and zk-optimized ISAs designed specifically to minimize proof costs.

RISC-V: General-Purpose Simplicity and Dominance

RISC-V is an open, modular, and minimal instruction set originally designed for conventional hardware processors. Its clean design, fixed-length instructions, and straightforward register model — with as few as 47 core instructions in its minimal base integer set (RV32I) — make it easy to implement, understand, and extend.

Strong Tooling and Developer Familiarity

For zkVMs, RISC-V offers a strong starting point thanks to its mature and robust tooling ecosystem. Developers can write high-level programs in Rust, C, or other mainstream languages and compile them to RISC-V almost seamlessly using LLVM backends.

This broad compatibility lowers barriers to adoption and allows teams to leverage existing debugging, profiling, and other tools. It also enables rapid prototyping and smoother transition from prototype to production. In practice, this means zkVM teams can focus more on optimizing their proving systems rather than reinventing basic compilation and developer workflows.

Challenges for SNARKs

Despite these advantages, RISC-V was not designed with SNARKs in mind. In a traditional silicon processor, registers allow fast local data access and reduce expensive memory operations. But in a zkVM, every register directly increases prover cost and proof size.

Moreover, dynamic control flow mechanisms such as conditional jumps and branches are highly efficient on hardware but become cumbersome in a zk context. Circuits must encode all possible branches and conditions to ensure correctness, which bloats the constraint system and slows down proof generation.

The Dominant Choice Among zkVMs

Despite its inefficiencies in proof generation, RISC-V has become the dominant architecture among zkVM implementations today. A large part of this adoption is due to the immediate benefits of developer familiarity and mature infrastructure. It also reflects a pragmatic approach: by prioritizing a widely supported ISA, zkVM projects can attract more contributors, integrate mature audit and testing pipelines, and build momentum toward mainnet deployment.

Most notably, nearly all zkVMs that aim to prove Ethereum mainnet blocks in real-time today are RISC-V based. This convergence shows that, for now, the trade-off heavily favors ecosystem reuse and standardization over theoretical proof efficiency.

MIPS: A Classic and Streamlined Alternative

MIPS is a classic RISC-style instruction set architecture, known for its simplicity and widespread use in academia and embedded systems. Even before the emergence of zkVMs, MIPS was appreciated for its minimal design and ease of analysis, which made it a frequent choice for teaching computer architecture.

Why MIPS for zkVMs?

In the context of SNARKs, MIPS offers a few appealing properties. Its extremely straightforward design and reduced instruction set can lower execution complexity compared to more feature-rich ISAs like RISC-V. Fewer instructions and simpler decoding logic mean that the corresponding zk circuits may have fewer constraints and slightly smaller execution traces.

For example, projects like zkMIPS (by ZKM) have chosen MIPS specifically to capitalize on these simplifications. By using MIPS, they aim to minimize the number of cycles needed and reduce overhead during proof generation, all while preserving a strong developer experience.

Moreover, MIPS has a long-standing, mature ecosystem and has been the basis for many teaching tools and simulators. For example, a program written in Rust, Go, or other high-level languages can be compiled into MIPS machine code. This history provides a foundation of reliable tooling and makes it easier to port or compile programs.

Limitations and Trade-offs

While MIPS offers a streamlined and simpler architecture than RISC-V, it still inherits a key limitation shared by most general-purpose ISAs: it was not designed with SNARKs in mind.

Even with its reduced instruction set, MIPS programs involve registers and explicit low-level control flow, which can lead to larger execution traces in a zk proof system. This ultimately results in higher prover costs and longer proof generation times than purpose-built zk-optimized ISAs.

Nonetheless, again, for many teams, these costs are offset by MIPS’s simplicity, mature tooling, and decades of accumulated knowledge. The trade-off often feels acceptable because it allows developers to leverage familiar compiler pipelines and focus on building applications rather than deeply optimizing circuits from scratch.

Cairo: A zk-Optimized ISA

Cairo, developed by StarkWare, represents a radical departure from conventional ISAs. It was not adapted for proofs but designed from the ground up as a SNARK-friendly CPU architecture. The goal was to create an instruction set that is inherently efficient to prove, which led to a design that re-imagines how instructions interact with memory, registers, and computation itself.

An ‘Algebraic RISC’ Instruction Set

At its core, Cairo’s ISA is an Algebraic RISC (Reduced Instruction Set Computer). This means its instruction set is minimal and its native data type is not a 32 or 64-bit integer, but an element in a finite field. The core instructions perform simple field arithmetic, like addition and multiplication. This “algebraic” nature is the key to its efficiency, as these instructions map directly and cheaply to the polynomial constraints of a SNARK proof.

Memory-by-Assertion and Instruction Format

The Cairo ISA fundamentally changes how instructions handle memory. It lacks traditional load and store opcodes for a read-write memory. Instead, its primary mode of memory interaction is a form of assertion. An instruction like [ap] = [fp - 3] + [fp - 4] is not just a computation; it is an assertion that the value in memory at the address ap must equal the sum of the values at the other two addresses. The memory itself is “non-deterministic,” meaning its entire state is provided by the prover. The ISA’s job is simply to enforce the consistency of these assertions.

This design is reflected in the instruction format. Cairo instructions don’t operate on general-purpose registers. Instead, instruction opcodes are encoded with offsets relative to two special-purpose address registers: the allocation pointer (ap) and the frame pointer (fp). This makes the instructions compact and their effect on the state easy to verify.

Extending the ISA’s Power: Hints and Builtins

While the core ISA is minimal, its practical power is amplified by two concepts that sit alongside it:

First, prover hints are not part of the formal ISA but are a crucial part of the programming model. They allow a prover to solve complex problems (like a division or a hash) outside the proof system, and then use the simple ISA instructions to efficiently verify the answer. The instruction set is thus focused on cheap verification, not expensive computation.

Second, builtins act as a form of ISA extension through memory-mapped I/O. For common but arithmetically complex operations (like range checks), a program uses standard memory-access instructions to interact with a dedicated memory segment. The builtin, which has its own optimized proof logic, enforces constraints on this segment. In this way, the simple core ISA can “invoke” powerful, pre-defined operations without needing dedicated complex instructions.

The Trade-off: An Unconventional Instruction Set

The payoff for this unique ISA is substantial: programs can be proven with significantly smaller execution traces and faster proof generation times. However, the trade-off stems directly from its unconventional nature. Developers must learn to program with an instruction set based on field arithmetic and memory-by-assertion. This requires a new way of thinking about computation, presenting a steeper learning curve than ISAs that are simple compilation targets for familiar languages.

Other zk-Native Custom ISAs: Valida and PetraVM

Recent zkVM research has produced new fully custom Instruction Set Architectures (ISAs) designed specifically for proof efficiency rather than silicon performance. Two strong examples are Valida and PetraVM.

Valida: Minimal and Register-Free Design

Valida takes a radically simplified approach to ISA design by removing all general-purpose registers. It uses only a minimal set of special-purpose pointers to manage control flow and stack frames. All local variables and intermediate data are managed on the stack or in memory.

This design choice dramatically reduces the number of columns in the execution trace and simplifies constraint systems, directly improving prover performance. Additionally, Valida introduces specialized instruction formats that combine related operations to reduce branching overhead and further minimize circuit complexity.

A key feature is its tight integration with high-level languages via a dedicated LLVM backend, allowing developers to write in familiar languages like C and compile directly to Valida’s streamlined, zk-optimized ISA.

PetraVM: Binary-Field-Oriented ISA

PetraVM is another custom ISA built specifically to leverage the advantages of binary-field SNARKs. Instead of using traditional register files, PetraVM’s ISA focuses on minimizing state and simplifying control flow at the instruction level.

Its instruction set is designed to be minimal and highly composable, using static function frames and strictly defined pointer arithmetic to reduce the complexity of branching and data manipulation. PetraVM supports a flexible and extensible instruction set, which can be expanded with additional operations without increasing baseline proof costs when unused.

This focus on a clean, minimal instruction set allows PetraVM to efficiently support advanced features like recursion and field arithmetic while keeping the prover workload low.

Hybrid and Intermediate Approaches: WASM and eBPF

Beyond purely general-purpose or purely custom ISAs, hybrid approaches also exist. One prominent example is WebAssembly (WASM). While WASM is not an ISA in the strict sense, it serves as an intermediate representation that many modern languages (including Rust and Go) can compile to. WASM features a formally specified stack model and predictable control flow, making it a convenient high-level target.

In zkVM design, WASM can serve as an initial compilation target, which is then further transformed into a zk-optimized backend representation. This approach combines the robust tooling and developer familiarity of WASM with the performance advantages of custom lower-level circuits. Some projects explore further introducing specialized stack or memory models (like Write Once Memory) during this transpilation step to optimize the final zk circuit.

eBPF, originally designed for high-speed sandboxed execution in environments like Linux and Solana, can be also considered. Its simplicity and efficiency make it attractive for certain use cases, but it has not yet been deeply explored in zk contexts, and its ultimate potential remains open for future research.

Balancing Efficiency and Compatibility

Choosing an ISA for a zkVM requires navigating a fundamental tension: optimizing for prover efficiency versus preserving compatibility with existing developer ecosystems and tools.

General-purpose ISAs like RISC-V and MIPS offer immediate integration with existing compilers and broad language support but come at a cost in proof size and generation time. In contrast, zk-optimized ISAs like Cairo, Valida, and PetraVM can achieve drastic improvements in proof performance but require new compilers, new developer education, and often a rethinking of programming paradigms.

Today, RISC-V has emerged as the dominant choice among zkVMs, not only because of its strong ecosystem and tooling maturity, but also due to recent advances that have dramatically improved its proving efficiency. Several zkVM projects have successfully achieved real-time proving of Ethereum mainnet blocks using RISC-V, demonstrating that its original proof inefficiencies can be effectively mitigated through careful circuit design and engineering optimizations.

Instruction Set Architecture thus shapes the core trade-offs in zkVM design. It dictates not only how programs are written and executed but also how efficiently and succinctly they can be proven.

ISA Comparison Recap

ISA	Pros	Cons
RISC-V	- Mature tooling and compiler support (LLVM) - Familiar to developers - Modular and extensible - Open source	- Originally not designed for proofs (many registers, dynamic control flow) - Larger constraint systems without optimization
MIPS	- Simple core design - Few instructions - Well-known in academia	- Still general-purpose (not zk-optimized) - Registers and branching still add overhead
Cairo	- Designed from scratch for zk efficiency - Algebraic field-based instructions - Minimal register logic	- New programming model - Steep learning curve
Valida	- No general-purpose registers - Simplified control flow - LLVM backend for easy adoption	- Requires custom compilers and circuits - Less general-purpose flexibility
PetraVM	- Binary-field-optimized - Minimal and composable instruction set - Supports advanced features like recursion	- Requires fully custom stack and new toolchains - Still early-stage adoption
WASM	- Very broad language support - Standard intermediate representation - Familiar to many developers	- Not a native ISA (requires transpilation for zk) - Proof system efficiency depends on backend design
eBPF	- Extremely simple and efficient bytecode - Proven in sandboxing contexts	- Not yet explored deeply in zk context - Limited tooling for zk

Arithmetization

Before a zkVM can prove a computation, it must first translate that computation into a language that cryptographic proof systems understand: the language of polynomials. This translation process is called arithmetization. It is the step that converts a statement about computational integrity, like “this program was executed correctly”, into an equivalent algebraic statement about a system of polynomial equations.

The core goal is to create a set of polynomial constraints that are satisfied if and only if the original computation was valid. Once we have this algebraic representation, the subsequent layers of the proof system, such as a Polynomial IOP, can take over to generate a succinct proof.

The Core Components: Execution Trace & Constraints

At the heart of arithmetizing a machine’s computation are two key components: the trace and the constraints that govern it.

The Execution Trace

The first step is to record the computation’s every move. This record is called the execution trace. Conceptually, it’s a table where each row represents the complete state of the virtual machine at a single point in time (a clock cycle), and each column represents a specific register or memory cell tracked over time.

For example, a simple computation that calculates a Fibonacci sequence would have a trace with one column, where each row n contains the n-th Fibonacci number. This detailed table is the execution trace.

To understand why this trace is also called the witness, it helps to step back and look at the general cryptographic meaning of the term. A witness is the secret data that a prover possesses that makes a public statement true. For a zkVM, the public statement might be “running this program with public input x results in public output y”. The witness is the answer to the question “how?”. It’s the complete set of intermediate variables and secret values that demonstrate the computation’s validity from start to finish.

Therefore, the execution trace (as a complete, step-by-step record of the machine’s internal state) is the concrete form this witness takes for a program’s execution. It is the core evidence the prover will use to construct the proof.

Clock Cycle (Row)	Register 0 (Column)
0	1
1	1
2	2
3	3
5	5
…	…

Constraints: The Rules of the Computation

An execution trace is only valid if it follows the rules of the computation. These rules are formalized as constraints, which are simply polynomial equations that must hold true.

Transition Constraints: These enforce the rules for moving from one state (row) to the next. For our Fibonacci example, the transition constraint is Trace[n+2] = Trace[n+1] + Trace[n]. This rule must be satisfied for every applicable row transition.
Boundary Constraints: These enforce conditions on the start and end states. In the Fibonacci example, a boundary constraint would be Trace[0] = 1 and Trace[1] = 1, fixing the initial state.

If every transition and boundary constraint is satisfied, the computation is valid. The power of arithmetization lies in expressing both the trace and these constraints using polynomials.

Arithmetization Schemes

Once a computation has been captured in an execution trace, the next step is to encode its correctness as a set of polynomial constraints. This encoding, called an arithmetization scheme, is the interface between the computation and the proof system. Different zkVMs adopt different schemes depending on the nature of the computation and the proof system they target.

We now describe the three dominant families of arithmetization: R1CS, Plonkish, and AIR.

R1CS (Rank-1 Constraint Systems)

R1CS is the classic circuit-based arithmetization used in many SNARKs. It turns a computation into a collection of simple algebraic constraints, each one shaped like a small multiplication gate followed by a subtraction. These constraints are then checked to ensure the computation was done correctly.

Each R1CS constraint has the form:

\begin{equation} (\mathbf{s} \cdot \mathbf{a}) \cdot (\mathbf{s} \cdot \mathbf{b}) = (\mathbf{s} \cdot \mathbf{c}) \end{equation}

or rearranged as:

\begin{equation} (\mathbf{s} \cdot \mathbf{a}) \cdot (\mathbf{s} \cdot \mathbf{b}) - (\mathbf{s} \cdot \mathbf{c}) = 0 \end{equation}

Let’s break this down:

$\mathbf{s}$ is the witness vector. It contains all the values used in the computation: inputs, outputs, and any intermediate results.
$\mathbf{a}$, $\mathbf{b}$, and $\mathbf{c}$ are vectors that select which elements of $\mathbf{s}$ are used in this constraint. They are usually sparse (mostly zeros), and act like masks.

This single constraint checks whether a product equals another value, based on selected parts of the witness. To represent a full computation, we create one such constraint for each small step, forming a kind of “circuit” of arithmetic gates.

Example: Computing $w = x^4$

We can’t do this in one step, because R1CS only supports one multiplication per constraint. So we break it into smaller steps:

First, compute $w_1 = x \cdot x$
Then, compute $w = w_1 \cdot w_1$

Each of these steps becomes one R1CS constraint. That means computing $x^4$ requires two constraints and one intermediate variable $w_1$.

Why Use R1CS?

R1CS is powerful because it’s simple and general-purpose: you can represent any computation this way, given enough constraints and intermediate variables. It’s the backbone of many SNARK proof systems like Groth16 and Marlin.

However, it also comes with limitations:

Rigid structure: Every operation must be written as a multiplication and subtraction. Even simple operations like XOR or range checks may require several constraints and helper variables.
Gadget overhead: To represent common programming features like conditionals, booleans, or comparisons, you need to build “gadgets”, i.e. small collections of constraints designed to implement that logic.

So while R1CS is a flexible and foundational technique, it can become inefficient for complex logic or memory-heavy computations. That’s where newer schemes like Plonkish and AIR offer improvements.

Plonkish Arithmetization

Plonkish arithmetization, used in systems like Plonk and UltraPlonk, builds on R1CS but introduces more flexibility. Instead of hardwiring each constraint into a fixed quadratic form, it views computation as a table of values (a trace), where each row represents one step of the computation. Constraints are then applied row-by-row using selector polynomials.

Key Features:

Custom Gates via Selectors: Instead of one fixed constraint form, Plonk allows general linear combinations of trace columns with selector polynomials:

\begin{equation} q_L \cdot a + q_R \cdot b + q_M \cdot a \cdot b + q_O \cdot c + q_C = 0, \end{equation}

where
- $a$, $b$, and $c$ are witness values from the current row,
- $q_L$, $q_R$, $q_M$, $q_O$, $q_C$ are selectors that define the operation.
This allows each row of the trace to act like a different type of gate, depending on the selectors: addition, multiplication… It reduces constraint count by unifying multiple operations under a single constraint form.
Wiring via Permutation Checks: Plonkish systems verify that outputs from one step are correctly reused as inputs in another using a permutation argument. Instead of tracking every connection manually, the prover shows that two lists (e.g., inputs and outputs) are just permutations of each other. This enables efficient wiring checks without complex gadgets.
Lookup Arguments: For operations like bitwise logic, comparisons, or range checks (which are expensive to encode algebraically) Plonkish systems allow the prover to simply lookup values from a precomputed table. The prover proves that its inputs match some row in a trusted dictionary of valid values (e.g., all valid (a, b, a ⊕ b) tuples for an XOR gate).

Together, these features make Plonkish systems more expressive than R1CS while remaining SNARK-friendly and efficient for a wide class of computations.

AIR (Algebraic Intermediate Representation)

AIR is the native arithmetization scheme used by STARK-based zkVMs. Rather than viewing computation as a circuit, AIR treats it as a sequence of machine states evolving over time. Each column of the execution trace corresponds to a register or memory cell, and constraints express algebraic relations between rows.

How AIR Works:

Trace Polynomials: Each column of the execution trace is interpolated into a univariate polynomial $P_i(x)$. This interpolation is performed over a specific subset of the finite field called the evaluation domain. To make the math efficient, this domain is chosen to be a cyclic multiplicative subgroup, which means it has a generator $g$ whose powers (e.g., $g^0, g^1, g^2, \ldots$) can produce every element in the domain. The input trace thus becomes a vector of polynomials:

$$ P_0(x), P_1(x), \ldots, P_{w-1}(x) $$
Polynomial Constraints: Transition and boundary constraints are expressed as polynomial identities involving shifted evaluations. For instance, the rule

$$ \texttt{Reg}_C[n+1] = \texttt{Reg}_A[n] + \texttt{Reg}_B[n] $$

becomes:

$$ P_C(gx) - P_A(x) - P_B(x) = 0 $$

where $g$ is a generator of the evaluation domain, representing a one-step shift in time.

To connect this to a real zkVM, imagine the trace has columns for the current instruction’s opcode and various machine registers. The polynomial constraints are responsible for enforcing the entire CPU instruction set. For instance:
- Instruction Logic: For a row where the opcode is ADD, a constraint enforces that the values from two source register columns sum to the value in the destination register column. This is often written conditionally, like $$\text{is_add_opcode} \cdot (P_{dest} - (P_{source1} + P_{source2})) = 0,$$ so the constraint only applies when the ADD instruction is active.
- Program Counter (PC): The PC register, which points to the next instruction, is also constrained. For most rows, the constraint is $$P_{PC}(g \cdot x) - (P_{PC}(x) + 1) = 0,$$ ensuring it simply increments. For a JUMP instruction, however, the constraint would change to enforce that the next PC value matches the jump destination specified in the instruction.
In this way, a complete set of polynomial constraints collectively describes the behavior of every possible instruction, ensuring the entire program execution is valid.
Quotient Argument: To prove that each constraint polynomial $C(x)$ is zero on its specific enforcement domain $D$, the prover uses an algebraic argument. They construct the vanishing polynomial $V_D(x)$ (which by definition is zero on all $x \in D$) and compute the quotient:

$$ Q(x) = \frac{C(x)}{V_D(x)} $$

If $C(x)$ correctly vanishes over $D$, then the division is clean and $Q(x)$ is a valid low-degree polynomial. If not, the division would result in a rational function (not a polynomial), and the prover’s dishonesty would be revealed. This process transforms the set of original constraint claims into an equivalent set of claims that each $Q_i(x)$ is a valid polynomial.
Composition Polynomial: Instead of testing each individual quotient polynomial $Q_i(x)$ for being low-degree (which would be inefficient), they are all merged into a single polynomial using random coefficients $\alpha_i$ provided by the verifier:

$$ C_{\text{comp}}(x) = \sum_i \alpha_i \cdot Q_i(x) $$

This single, randomly-combined composition polynomial is what the proof system ultimately tests. If this final polynomial is low-degree, it implies with very high probability that all the individual quotient polynomials were also low-degree, and thus all the original constraints were satisfied. This polynomial is then passed to a protocol like FRI for a final low-degree test.

Note on Multilinear Polynomials: While treating each column as a separate univariate polynomial is common, more modern AIR-based systems can view the entire execution trace as a single multilinear polynomial. As described in recent work on Jagged Polynomial Commitments, this approach allows the system to commit to the entire trace as one object, which can drastically reduce the verification cost and prover overhead associated with managing many individual column commitments.

AIR’s tight alignment with machine semantics, support for high-degree constraints, and STARK-compatibility make it the arithmetization of choice for zkVMs that prioritize scalability and transparency.

Resources for Further Information

Information Theoretic Layer: IOPs and Poly-IOPs

After a computation has been transformed into an Algebraic Intermediate Representation (AIR), which defines the set of mathematical rules (as polynomial equations) that a valid computation must follow, the next challenge is for the prover to convince a verifier that they possess a valid execution trace, the table recording the machine’s state at every single step, that satisfies these rules.

The primary framework used here is the Interactive Oracle Proof (IOP). This entire process represents the middle layer of the modern SNARK design paradigm: first arithmetization, then this information-theoretic protocol, and finally cryptographic compilation.

Interactive Oracle Proofs (IOPs)

The IOP model is a powerful generalization of the earlier concept of Probabilistically Checkable Proofs (PCPs), designed to be more efficient for building practical proof systems. An IOP is a formal protocol between a prover and a verifier that proceeds in rounds:

The prover sends a message to the verifier. In the IOP model, this message is treated as an oracle, a function that the verifier can query but not read in its entirety.
The verifier receives the oracle and, based on previous messages, generates a random challenge and sends it to the prover. The verifier can also make a limited number of queries to the oracles it has received.
This interaction may continue for several rounds. Finally, the verifier decides whether to accept or reject the proof based on the query results.

The key property of an IOP is that its security is information-theoretic. This means that a computationally unbounded prover cannot cheat the verifier, except with a negligible probability. The security comes from the verifier’s randomness, not from any cryptographic hardness assumption.

Polynomial IOPs (Poly-IOPs)

For zkVMs, we use a specific and highly effective type of IOP called a Polynomial IOP (Poly-IOP). In a Poly-IOP, the oracles sent by the prover are guaranteed to be low-degree polynomials.

This Poly-IOP model is a perfect match for the AIR arithmetization:

The columns of the execution trace are interpolated into polynomials.
The polynomial constraints of the AIR become polynomial identities that must be proven (e.g., A(x) + B(x) - C(x) = 0).

A Poly-IOP provides the formal steps to prove these identities. For instance, to check if two polynomials P(x) and Q(x) are identical, the verifier challenges the prover with a random point r from a large field and checks if P(r) = Q(r). According to the Schwartz-Zippel Lemma, if the polynomials are different, this check will fail with overwhelming probability. STARK proof systems, for example, are fundamentally highly optimized Poly-IOPs.

The following figure is taken from zk-SNARKs: A Gentle Introduction and illustrates the prover-verifier interaction in a PIOP:

PIOP

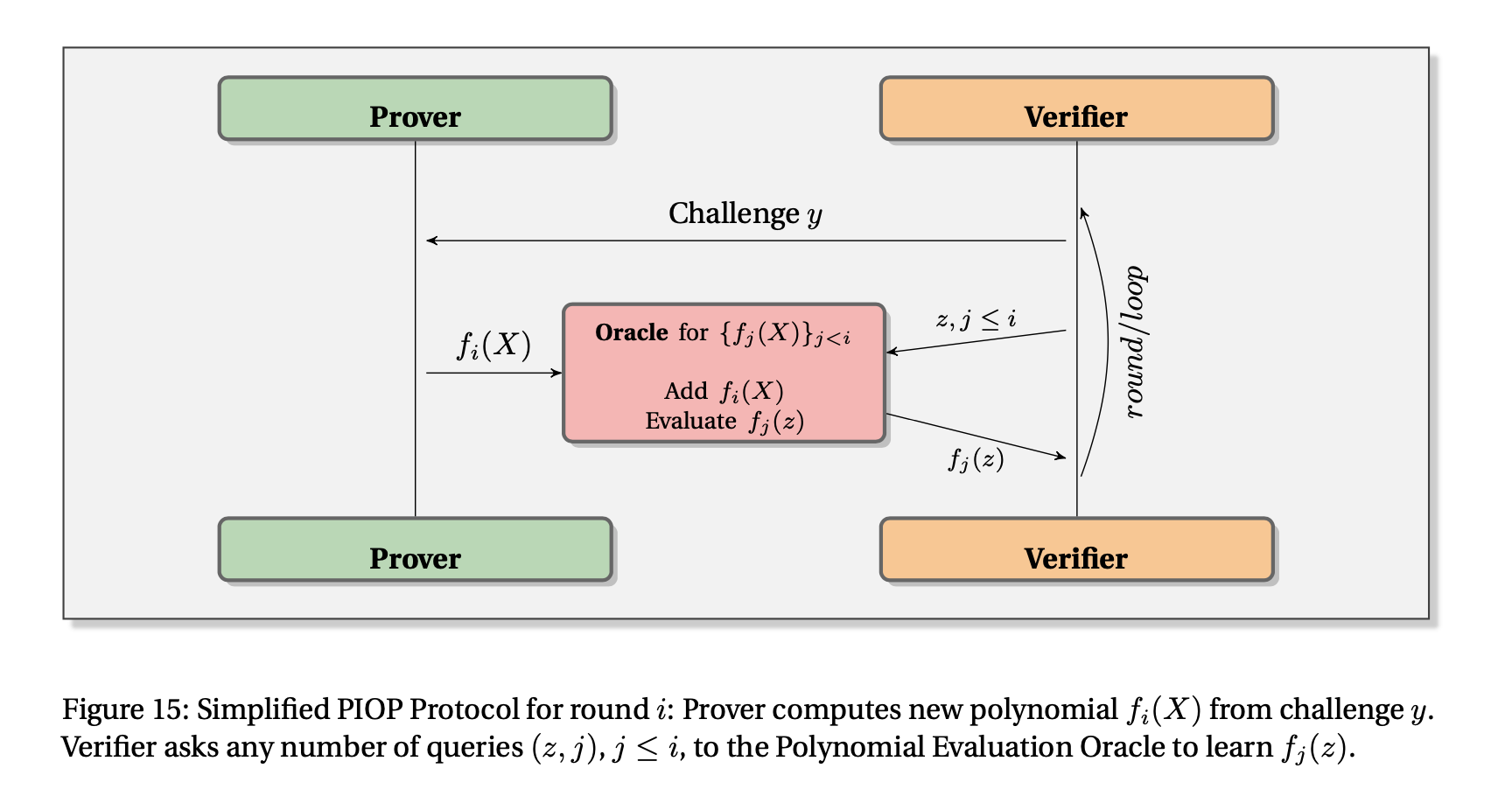
The Bridge to Concrete SNARKs

An IOP is an abstract mathematical protocol, not a practical proof system. To turn a Poly-IOP into a concrete, real-world SNARK, a process often called a cryptographic compiler is applied using two main tools:

Polynomial Commitment Schemes (PCS): Instead of sending entire polynomials as oracles (which would be huge), the prover sends a small, cryptographically-binding commitment to each polynomial. The PCS then allows the prover to generate proofs that the committed polynomial evaluates to a certain value at specific points, which the verifier can check. This is how succinctness is achieved. The choice of PCS is critical, as it directly determines many properties of the final SNARK. For example, using KZG results in a system with a trusted setup, while using FRI results in a transparent (setup-free) and quantum-resistant system.
The Fiat-Shamir Heuristic: To eliminate interaction, the verifier’s random challenges are replaced with the output of a cryptographic hash function. The prover simulates the interaction by hashing their own previous messages to generate the next “random” challenge for themself. This makes the proof non-interactive.

This modular design is at the heart of most modern SNARK constructions and provides a flexible blueprint for building new proof systems.

Cryptographic Layer: Polynomial Commitments

Note. Section under construction. Section may be deleted or just filled with links to literature on poly coms.

Cryptographic Layer: The BCS Transform

The IOP is a powerful framework for proving a computation’s integrity, based on a multi-round conversation between a prover and a verifier. While theoretically robust, this protocol is an abstract blueprint with two features that make it impractical for real-world use on Ethereum:

It is interactive, requiring a back-and-forth dialogue.
Its messages are enormous, as the prover’s “oracles” are very large.

Ethereum requires a proof to be a single, compact piece of data that can be verified quickly without any further communication. To bridge this gap, we use a cryptographic compiler to convert the abstract IOP into a concrete, non-interactive proof. The most influential method for this is the BCS Transform, named after its creators, Ben-Sasson, Chiesa, and Spooner. It provides an elegant and reliable process for turning an interactive protocol into a single, verifiable argument, denoted as $\pi$.

Core Cryptographic Tools

The BCS transform achieves this conversion by integrating two fundamental cryptographic techniques: the Fiat-Shamir heuristic to eliminate interaction and Merkle trees to compress the proof data.

The Fiat-Shamir Heuristic: Eliminating Interaction

In an IOP, the protocol advances when the verifier sends a random message, or challenge, to the prover. The Fiat-Shamir heuristic is a method to make this process non-interactive.

Instead of relying on a live verifier, a prover in a public-coin protocol can generate these challenges for himself in a way that is both deterministic and publicly verifiable. This is accomplished using a cryptographic hash function. The prover takes the entire public transcript of the interaction so far (including public inputs and commitments from previous rounds) and hashes it. The resulting hash output serves as the verifier’s random challenge for the current round.

Since the hash function is deterministic, anyone can re-compute the same challenges from the same transcript, ensuring the prover cannot cheat by picking favorable challenges. This technique effectively removes the need for a verifier to be present during proof generation, turning the interactive dialogue into a non-interactive process that the prover completes on its own.

Merkle Trees: Compressing Proof Data

The second challenge is the immense size of the prover’s oracle messages. For instance, an oracle can be a list containing millions of polynomial evaluations. Transmitting such a list is impractical.

Merkle trees solve this by allowing the prover to commit to a large dataset with a single, small hash value known as the Merkle root. The prover places all the values of its oracle message at the leaves of a Merkle tree and generates the root, which now serves as a succinct commitment to the entire oracle.

When the verifier needs to check the value at a specific position (a query), the prover provides only two things:

The value at that specific position (in green in the following diagram).
A short authentication path, which consists of the sibling hashes along the path from the value’s leaf to the tree’s root (in blue in the following diagram).

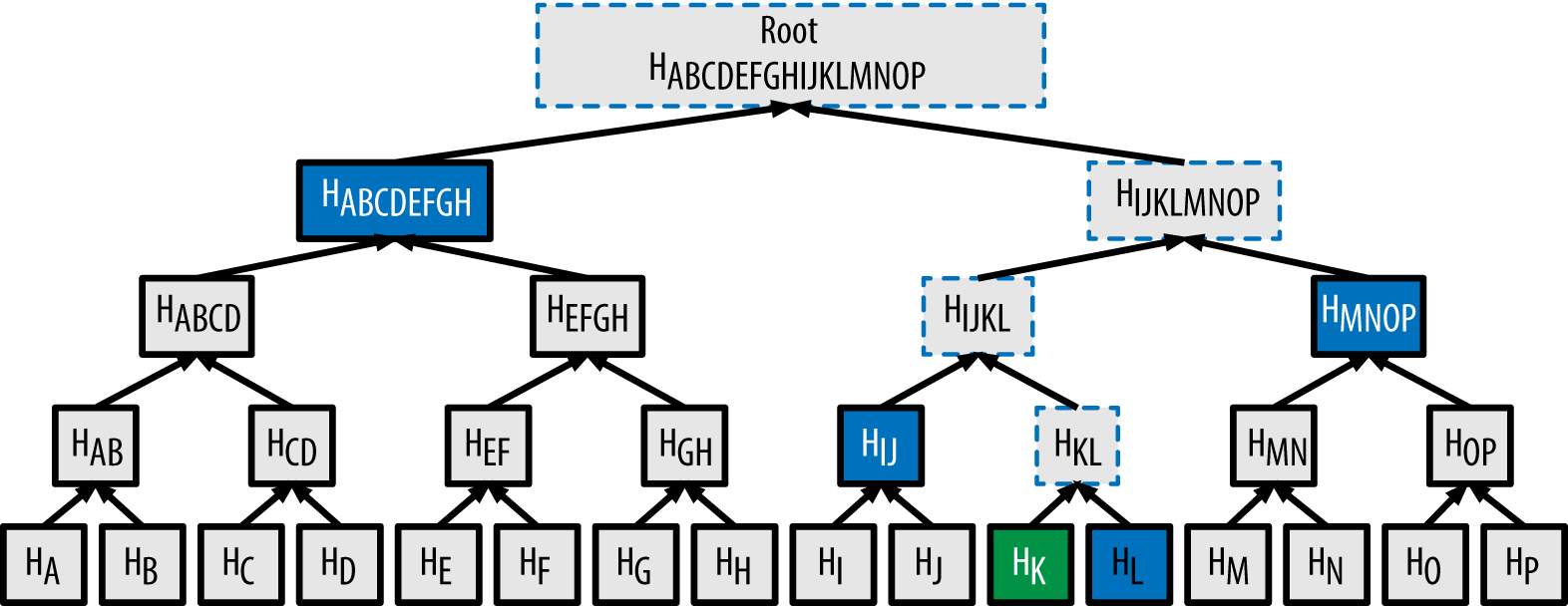
Merkle Tree

Using this path, the verifier can re-compute the root and confirm that the provided value is a genuine part of the dataset to which the prover originally committed. This enables succinct verification of oracle data without transmitting the oracle itself.

The Complete Transformation Process

The full BCS transform combines these two components into a sequential process. The prover simulates the entire IOP internally, round by round, to construct the final proof string $\pi$.

Here is the step-by-step flow:

Round 1 begins: The prover takes the public input $x$ and hashes it to generate the verifier’s first challenge, $m_1$. $$m_1 = HASH(x)$$
Prover responds and commits: Using the challenge $m_1$, the prover computes its first oracle message, $f_1$. It then builds a Merkle tree over $f_1$ to produce the first Merkle root, $rt_1$.
Chaining the rounds: This step for ensures the integrity of a multi-round protocol. To begin the next round, the prover creates a new protocol state by hashing the new Merkle root with the state from the previous round. $$state_1 = HASH(rt_1 || x)$$ $$m_2 = HASH(state_1)$$

This cryptographic chaining creates a verifiable, ordered sequence. The challenge for round 2 ($m_2$) depends on $state_1$, which in turn depends on the commitment from round 1 ($rt_1$). This makes it impossible for a malicious prover to alter the logic or order of the protocol’s rounds without breaking the hash chain. This process is where the binding property of the Merkle tree comes in: once the prover uses $rt_1$ to generate the challenge for the next round, they are cryptographically bound to the original oracle message of round 1 and cannot change it. This process is repeated for all $k$ rounds of the IOP: $$state_i = HASH(rt_i || state_{i-1})$$
Finalizing the proof: After the last round, the prover uses the final state, $state_k$, to deterministically generate the positions of all the verifier’s queries. The prover then assembles the final proof $\pi$, which contains:
- All the Merkle roots $(rt_1, rt_2, …, rt_k)$.
- The values and their corresponding authentication paths for each query.

The verifier receives this single, compact string $\pi$. To validate it, the verifier performs the same sequence of hash computations to regenerate all the challenges and states. It then uses the authentication paths provided in the proof to check if the prover’s answers are consistent with the Merkle root commitments for each round. If all checks pass, the proof is accepted.

Security Implications of the Transform

The BCS transform is highly effective, but it introduces a fundamental shift in the security model. The original IOP possesses information-theoretic security, which means that not even a computationally unlimited prover can cheat. The resulting SNARK, however, has computational security.

Its soundness now relies on a cryptographic assumption that the hash function used is secure. The specific security model for this context is the Random Oracle Model, which treats the hash function as an idealized mathematical object. For a formal definition of this model and its implications, we refer the interested reader to the cryptographic literature (A Graduate Course in Applied Cryptography by Dan Boneh and Victor Shoup, is a good source of information about this).

This shift from an interactive dialogue to a non-interactive proof introduces a new theoretical vulnerability. Because the prover now generates the challenges himself using a hash function, a malicious prover with sufficient computing power could try to “grind” on that function. Grinding is a brute-force attack where the prover rapidly tests slightly different inputs, hoping to find one that produces a “lucky” hash output, i.e. a challenge that makes it easy to create a convincing proof for a false statement.

This non-interactive attack is the direct equivalent of a state restoration attack on the original interactive protocol. In a state restoration attack, a prover would theoretically “rewind” the verifier to a previous step to receive a new random challenge, repeating this until they get a lucky one. Grinding simply accomplishes the same goal without a live verifier.

Consequently, the security of the final non-interactive proof is fundamentally limited by the underlying IOP’s resilience to these state restoration attacks. This establishes a clear and measurable link: if the original interactive proof is weak against rewinding attacks, the compiled SNARK will be weak against grinding attacks.

This understanding is important because it allows for a modular design. Protocol designers can focus on creating an abstract IOP that is provably robust against state restoration, knowing that the BCS transform can then reliably compile it into a practical and secure non-interactive proof.

Security Considerations

Security is critical to the success of zkEVMs, especially as they move toward becoming part of Ethereum’s core infrastructure. To ensure a safe and resilient transition, the Ethereum community plans a phased rollout: zkEVM proving will be optional at first and become mandatory only once systems have been thoroughly vetted. Diversity is also a cornerstone of this approach—we aim to support multiple independent zkEVM clients so that if one encounters issues, others can continue to provide correct proofs. To guide this effort, there is a proposed set of security guidelines rooted in best practices from the broader cryptography and software industries, helping projects design, implement, and evaluate zkEVMs with robustness in mind.

Understanding Knowledge Soundness

The goal of a zkEVM is to ensure that when someone claims they executed some EVM bytecode, they really did. That is, if a proof says “this transaction was processed correctly,” we should be confident that the prover knows how that transaction was executed. This property is called knowledge soundness, and it’s what prevents malicious provers from fabricating proofs out of thin air.

To achieve this, zkEVMs are built in layers. Here’s roughly how that structure looks:

The EVM bytecode is run through a virtual machine using a low-level instruction set (an ISA).
That execution is arithmetised into a set of algebraic constraints.
An Polynomial Interactive Oracle Proof (Poly-IOP) is used to check that those constraints are satisfied.
The Poly-IOP is compiled into an interactive argument using a polynomial commitment scheme.
Finally, the protocol is made non-interactive using the Fiat-Shamir transform, so it can be verified with just a single message.

The first three layers—the ISA execution, the constraints, and the Poly-IOP—are designed to be information-theoretically sound. That means, assuming everything is implemented correctly, even an attacker with infinite computing power couldn’t forge a convincing proof. This is a very strong guarantee, but it only holds in the idealised interactive world where the verifier has access to imaginary oracles.

To make this practical, we compile the Poly-IOP using cryptographic primitives. We replace idealised oracles with real-world polynomial commitment schemes. At this point, we step into the realm of computational assumptions. For the compiled zkEVM to remain knowledge sound, the underlying polynomial commitment scheme (PCS) must satisfy two crucial properties:

Evaluation binding: once the prover commits to a polynomial, they can’t later claim it evaluates to something else.
Knowledge extractability: if the prover can convince the verifier of a claim, there must be a way to “extract” the polynomial they committed to.

The last step is to eliminate interaction entirely. This is done using the Fiat–Shamir transform, which replaces the verifier’s random challenges with deterministic hashes of the proof transcript. By removing interaction, the resulting proof becomes non-interactive and publicly verifiable. This is essential for systems like Ethereum, where the prover and verifier cannot interact directly. We must assume the hash function behaves like a random oracle, which is a strong heuristic assumption. Some systems target the Quantum Random Oracle Model (QROM) to prepare for potential quantum threats.

Putting it all together: the early layers of the zkEVM stack provide strong, ideal-world guarantees. The later layers compile those guarantees into something practical and succinct, grounded in well-studied cryptographic assumptions. If each layer is carefully constructed, we get a system where every accepted proof genuinely reflects a valid execution—succinctly, securely, and efficiently.

Knowledge Soundness in the Literature

The above structure for building knowledge-sound zkEVMs appears across many modern proof systems.

Marlin builds a Poly-IOP for the Rank-1 Constraint System (R1CS) and compiles it into a SNARK using the KZG polynomial commitment scheme. Knowledge soundness in Marlin depends on the extractability of KZG and the security of the Fiat-Shamir transform in the Random Oracle Model.
Binius constructs a multilinear polynomial commitment scheme suitable for polynomials over binary fields. They apply their PCS to a binary variant of the Plonkish constraint system, enabling efficient proof systems even in tiny fields.
WHIR, BaseFold, and FRI construct IOPs of proximity, which are used to verify that a function is close to one satisfying a set of algebraic constraints. These protocols form the basis for building prover-efficient polynomial commitment schemes, often used in STARKs.
Jolt focuses on the RISC-V virtual machine. It arithmetises RISC-V execution using lookup arguments and instantiates them via Lasso, which itself is built using polynomial commitments.

In all of these protocols, the same layered pattern appears: an interactive, information-theoretic proof at the foundation, compiled into a cryptographic argument using polynomial commitments and the Fiat-Shamir transform.

Targeting 128 Bits of Security

Before proving becomes mandatory on Ethereum L1, zkEVM systems are expected to achieve at least 128 bits of security. This level of assurance ensures that even powerful, well-resourced adversaries cannot forge proofs or compromise the integrity of the system. During the initial rollout—where proofs may be optional and value at risk is low—some projects may temporarily operate at lower thresholds (e.g., 100-bit security) to test APIs and proving infrastructure. But the target remains clear: 128-bit security is a requirement before mandatory proving can be considered safe.

So what does 128-bit security mean? In cryptographic terms, it means that any adversary’s probability of successfully breaking the system per unit of time is bounded by $2^{-128}$. More formally, if an attacker has an advantage $\epsilon$ after spending time $t$ trying to break the system, then 128-bit security requires that $\epsilon / t \leq 2^{-128}$. This benchmark reflects what the cryptographic community considers a safe margin, even against nation-state level adversaries.

To put this in context, NIST’s guidelines on key management cite 128 bits as the minimum acceptable security level for long-term use, particularly for systems intended to remain secure beyond 2031. This standard underlies a wide range of protocols and systems, including AES-128, elliptic curve cryptography over 256-bit fields, TLS, IPsec, and others.

For a concrete sense of what’s computationally feasible, consider Bitcoin mining. As of 2025, the most difficult known Bitcoin block (Block 756951) had a hash with 97 leading zero bits. Statistically, achieving such a result requires around $2^{97}$ SHA-256 evaluations in expectation. This gives a tangible measure of the scale of effort possible with globally distributed hashpower.

Measuring Bit Security in zkEVMs

Assessing the bit security of a zkEVM means understanding how soundness can degrade through each layer of the system. Even if individual components are secure, the overall system may be weaker when composed. Key contributors include:

Challenge soundness in the Poly-IOP
The verifier sends random challenges to the prover. If these are predictable or repeatable, an adversary may get “lucky” and bypass detection. Bit security here depends on the size of the field the challenges are sampled from.
Polynomial commitment scheme (PCS)
Most zkEVMs rely on polynomial commitments to compile their Poly-IOP into a SNARK. The bit security of the system is bounded by the hardness of opening a commitment inconsistently.
Hash function assumptions (Fiat-Shamir)
The Fiat-Shamir transform replaces verifier randomness with hash outputs. Soundness here assumes the hash behaves like a random oracle, which is a heuristic assumption. Bit security is typically estimated from the preimage or collision resistance of the hash function, though it’s often slightly weaker in practice due to modeling gaps.
Grindability of Fiat-Shamir
In some systems, adversaries can try multiple inputs to the hash function—called grinding—to find a challenge that helps them cheat. If the success probability per attempt is $p$, and the adversary can try $n$ transcripts then the overall success probability is bounded by $p \cdot n$. In multiround protocols with many Fiat-Shamir challenges, this attack can reduce the effective bit security.

In practice, the total bit security of a zkEVM is limited by its weakest link. Even if most components offer 128-bit security, a single step with only 110 bits of assurance could lower the system’s effective strength. Because of this, security analysis should account for all components, their assumptions, and how they compose.

Specification and Formal Verification

For zkEVMs to be secure, two things must hold: the cryptographic security proof must be correct, and the implementation must match the scheme that was proven secure. These are both difficult to guarantee in practice. For example, a critical flaw was recently discovered in the Plonky3 FRI verifier—despite the underlying theory being sound. One of the most useful tools for bridging this gap is a written specification. A good specification is the foundation for both verification and auditing.

Specifications serve three critical roles:

First, they allow implementers, auditors, and researchers to understand what the system is supposed to do without needing to reverse engineer the codebase.
Second, they allow us to formally verify that the implementation matches the intended design, and that this design aligns with the cryptographic scheme that has been proven secure.
Third, they enable interoperability, allowing other codebases to include compatible but distinct implementations.

Specifications become especially important when optimisations are applied. Performance tweaks often restructure or rewrite parts of the system in non-obvious ways. Without a spec, it is difficult to tell whether such changes preserve correctness—or whether they introduce subtle inconsistencies that break the soundness of the whole.

The Ethereum Foundation is currently leading the Verified ZK-EVM initiative, which supports the use of formal methods across the Ethereum ecosystem. The most important step zkEVM projects can take to support this effort is to write high-quality, accurate, and unambiguous specifications—with clear semantics and deterministic behavior.

Formal methods are widely used in high-stakes engineering: from aircraft control software, to CPU instruction set verification, to operating system kernels. zkEVMs, which aim to secure smart contract execution on Ethereum’s base layer, face similar stakes. On this topic, the following xkcd seems highly relevant.

Security Conclusions

As zkEVMs mature from experimental prototypes into core components of Ethereum’s infrastructure, security must be treated as a first-class concern. Achieving this requires more than just strong cryptographic building blocks—it also demands rigorous security proofs, clear specifications, careful engineering, and a realistic understanding of what can go wrong when these pieces are composed.

Overview of Architectural Choices

Team	zkVM	ISA	SNARK system
Brevis	Pico	rv32imc	P3 lib (and gnark?)
Succinct	SP1 Hypercube	rv32im (SP1)	P3 lib (SP1)
ZKM	Ziren	mips32r2	P3 Lib
ZisK	ZisK	rv64ima tested ( but rv64gc here?)	PIL2 Proofman Lib
MatterLabs	Airbender	rv32im	Custom
Axiom	OpenVM	rv32im	P3 Lib
RISC Zero	R0VM	rv32im	Custom
a16z	Jolt	rv32im (more?)	Custom

Part III: Practical Guides

Note. Section under construction.

this part should tell the reader how to start playing around with zkEVMs.
for example, it could refer to ere
we should also talk to different audiences in different subparts (client devs, …)

Benchmarking

When considering using zero-knowledge technology at the L1 of Ethereum, it is required to do a thorough evaluation of how it will impact the network properties and requirements. In this chapter, we explore in detail how using zkVMs can be evaluated by doing proper benchmarking to gain an understanding of this front. A similar summary of this chapter can also be found in the following video section.

Why?

When introducing a new technology or a big protocol change in Ethereum, we need to understand the implications on multiple fronts, for example:

Does it fit the desired hardware specs for the node types that will be involved?
How can actors in the network (e.g. provers) understand how different hardware configurations behave? (e.g. GPU models’ power efficiency).
What new risks are introduced regarding liveness and security?
Are there any blockers to using this technology? (i.e. non-obvious protocol changes)

To answer these questions, we can’t take a theoretical approach with napkin math, since usually the answer depends on many engineering dimensions of the solutions, e.g. how optimized are the implementations, unexpected limitations compared to theoretical possibilities, maturity, etc. Said differently, (some) devils might be in the details.

Moreover, there are many practical aspects that we need to consider:

We’re early in the process of deciding which are the best-performing and mature zkVM implementations — we need a quick way to evaluate all existing and easily introduce new options.
Each zkVM implementation is moving at a fast pace, so it is mandatory to understand their performance improvements and quickly catch potential regressions.
Depending on the performance of each zkVM, we can envision trying to pair less optimized EL guest programs with more optimized zkVMs to have a balanced suite of combinations for having the most reliability.

Building a zkVM benchmarking pipeline designed specifically for Ethereum needs is a great tool to achieve our goal in the best way possible.

Note also that proving a block with zkVMs depends on two factors: the zkVM used for execution/proving, and the EL client used as a guest program. While all EL clients implement the same protocol rules, they are programmed in different languages and compiled with different tools thus the final bytecode executed in the same zkVM can have different properties/performance. Being able to benchmark the EL clients dimension is as relevant as the zkVMs dimension.

Finally, this effort wouldn’t only help Ethereum core developers to evaluate and implement any required protocol changes, but also provide concrete guidance to zkVM teams to keep optimizing the most performance-critical cases.

How?

zkVMs are general constructions to prove generic programs that can be compiled to any ISA supported by them. This means that the Ethereum use-case is a subset of programs that they support proving. We are not interested in doing general zkVM benchmarking, but focusing on Ethereum block validation (i.e. benchmarking a program calculating the Fibonacci sequence isn’t interesting).

zkVM benchmarking for Ethereum means putting at the center fixtures that represent any valid block that can happen in the protocol, which we can separate into two main buckets:

Average cases: these cases can be represented by mainnet blocks — this can help understand the performance in the average cases.
Worst cases: these cases cover very rare cases that naturally happen in mainnet, or specifically designed blocks by attackers to affect the chain’s liveness. A common term to describe them is prover killers.

Understanding both cases is crucial to evaluate potential protocol design changes (e.g. gas cost models or incentives).

Benchmarking different zkVMs can become a hot topic since it directly puts different zkVMs face-to-face. These teams work incredibly hard to provide the best version of their design, so it’s important to be responsible in doing a fair comparison. For this reason, the benchmarking pipeline should be transparent and also easily reproducible.

Protocol design relationship with zkVMs

At the center of zkVM benchmarking is designing the cases that we should run in the zkVM and EL client combinations — we call this benchmark fixtures. To do a meaningful design of which fixtures are run, we need to understand the full protocol in detail, so as to have enough coverage of relevant ones to benchmark.

Before jumping into deeper details, it is helpful to understand what exactly is being proven by zkVMs for the Ethereum use-case. The guest program execution is an EL client executing a stateless block validation. This means receiving as inputs a block plus a witness with the required Ethereum state, and executing the block to check if the post-state root, gas usage, and other fields are valid (i.e. that the state transition function was correct).

When a block is executed, we can separate the workload into two main buckets:

Non-EVM execution: executing a block has many tasks that do not depend on the EVM. For example, recovering senders from transactions, processing withdrawals, system contract tasks, etc.
EVM execution: this covers the bulk of the block execution, which is the execution of transactions that call smart contracts.

This means that we need benchmark fixtures covering relevant workloads for both cases. For example, we need to understand how a block with the biggest amount of transactions possible behaves regarding recovering senders from transaction signatures. Or how a block using all the gas limit, calling the KECCAK opcode works.

Since the EVM execution is usually related to the bulk of the work when executing a block, it can also be helpful to consider the following dimensions:

Pure computation opcodes: EVM instructions that are pure computation can have different throughput when executing inside the zkVM. For example, ADD and MULMOD do not have the same cost.
Storage accessing opcodes: many opcodes main load involve accessing state. Recall that zkVMs prove a stateless execution of a block validation; thus, there’s no real disk access involved in the execution. The relevant part of storage accessing opcodes is computational tasks related to verifying the state in the witness, which usually involves state tree proof verifications. This workload usually involves heavy computations for zkVMs, such as proving hashes.
Precompiles: EVM precompiles are optimized constructions within the EVM to do heavy cryptographic tasks, such as recovering a public key from a signature, or doing elliptic curve operations. Cryptographic-related tasks are usually very heavy operations for zkVMs, so having thorough coverage is mandatory.
Bytecode access: when a smart contract is executed in the EVM, we not only require executing instructions or precompiles, but also fetch and prove that the actual code being executed is correct. Currently, smart contract bytecode isn’t chunkified, so this opens a potential DoS vector that is very relevant to cover.

At the start of 2025, core developers started working on a big project to include benchmark tests in the execution-spec-tests repository. Before this effort, this repository contained an incredibly valuable set of correctness tests that had been the basis for the Ethereum zero-downtime reality. Now, benchmarks were also introduced that cover scenarios in all dimensions described above. These benchmark fixtures are not only useful for zkVM benchmarking but also for benchmarking raw execution in EL clients.

Tools

The zkEVM team within the EF has been working on a specific set of libraries and tools to support this initiative. The two main ones are ere and zkevm-benchmark-workload. The former is a Rust library that provides a single API to run guest programs in many zkVMs. This allows us to abstract many of the complexities of running guest programs. The latter is a tool that uses ere, specifically designed to run Ethereum fixtures for benchmarking, e.g. run EEST benchmarks, mainnet blocks, and experimental programs.

We won’t go into full detail in this chapter on how to use these tools since both have extensive documentation in the repository. Anyone is invited to use these libraries and tools and collaborate on making them better. For example, new zkVMs can integrate into ere and immediately have a complete toolset to benchmark how Ethereum would behave in them.

The strategy used in this style of benchmarking is running real mainnet blocks, specifically crafted to target known potential attacks, or using all the gas limit in a single opcode or precompile, each under a different scenario. For example, SSTORE and SLOAD can generate different workloads if they access hot and cold data, or the modexp precompile underlying implementation can be sensitive to particular inputs.

When the benchmarking fixture is targeting a block that uses all the gas limit for some pure computation opcode (e.g. ADD, MUL, MULMOD, etc), the overhead of pre/post block processing compared to the main block execution should be very low, and is amortized the bigger the gas limit. Note that some opcodes, like SSTORE, SSLOAD, EXTCODESIZE involve accessing state, thus including the pre/post block workload of reading/verifying and writing into the state tree must be considered part of the benchmark run.

It is also possible (and might be desirable for some reasons) to fully isolate some particular opcodes or precompiles by only benchmarking isolated EVM opcodes implementations, but this strategy can end up being too focused on a specific implementation compared to having a shared setup that we can run in all EL EVMs. Also, if we extract the cycles/cost of proving an empty block, we can get close to a very fair take on which opcodes or precompiles can be mispriced or problematic, at least in a relevant order of magnitude. Again, this other strategy shouldn’t be discarded, and both can be complementary.

Results

The EF zkEVM team is currently running the fixtures and collecting the results. Many parts of the stack are still changing at a fast pace (e.g. guest program optimizations, zkVM SDKs, etc). If you want to track early run results, they are being uploaded to this repository. Other websites, like Ethproofs, are planning on presenting results about worst cases using the same tooling and benchmark fixtures — so stay tuned.